テレパシーが教える１＋１　おかき編

こんにちは。テレパシー情報屋の加藤です

私も含めた現代人は１＋１の正しい回答も知りません。

知的レベルが非常に低いのです。

ここで言う知的レベルが非常に低い人たちは有名大学を首席で卒業した人たちや、ノーベル賞を受賞した科学者なども含みます。

３級だったテレパシーの実力が２級に近づいてい来ているのかもしれません。最近私は世間の有識者の言っていることがとても退屈に聞こえるようになってきているのです。

今回はそんな私も含めた知的レベルの低い皆さんに１＋１の正しい回答を教えましょう。

１＋１＝たくさん

文章題問題

問題：左手の上におかきが一つ乗っています。 右手の上にもおかきが一つ乗っています。 左手の上にあるおかきを右手の上にあるおかきに向けて「１＋１！」などと叫びながらたたきつけました。右手の上のおかきはいくつになりますか。

解答は↓↓↓

最近書いた記事：ＦＦの新作はこうやって作ると面白くなる１４｜テレパシー情報とMMOの話

解答

右手のおかきも左手の上に乗っていたおかきも粉砕されました。この出来事を数学ではどう解釈し、数式にするか？　解釈が分かれそうです。

※本当は右手からこぼれ落ちたおかきの分も計算に入れる必要があるでしょう。もう記事を書き終わってしまって今思い出したので、今回は入れないことにします。そのうちこぼれ落ちることについての記事も書くかもしれません。いや、そうじゃなくて、定義の仕方がダメなのか。数学上は無限の大きさと広さを持った手のひらがあり、その上にすべてのおかきの破片が乗っていることにしないとだめでしょうね。なんてご都合主義なんだ。

解釈１

一つ目は「一つ一つにおかきとしての特性が残る説」です。

解答：１＋１＝たくさん

本人は「１＋１！」と叫んでいたので仮に、本人の意思を尊重しておかきとおかきを衝突させる過程を１＋１であると捉えてみましょう。

「いくつ」と聞いてきたので個数を答える問題です。

粉々になったおかきの一つ一つがいまだにおかきとしての特性を持ち続けているとする説によると、粉々のばらばらになった部分部分の数だけおかきは存在していることになります。

おかきの数は多すぎて、細かくなりすぎてとても数えきれるものではありません。

よって１＋１の結果としておかきはたくさんになったのです。

１＋１＝粉々とか１＋１＝ばらばらとかの回答もあるでしょう。

「千の風になって」的な世界観を感じますね。詩的です。衝突からの崩壊現象についてシンプルに扱ったこの計算は、スポーツ選手などの筋肉を崩壊させることを仕事にしている人たちにも役立つでしょう。

解釈２　

２つめは「もはやおかきではない説」です

解答：１＋１＝０

頑固なことに粉々になったおかきはもはやおかきではないと考えるようです。手の上には未だに粉々になったおかきがあります。にも関わらずその実在を完全に無視して、定義上おかきに該当する物体がない以上はゼロだと数えるのです。理知的な性格なのでしょうか。さばけていますね。

エビデンスに基づかないといけない状況で役立つ可能性があります。粉々になったおかきが未だにおかきであるという科学的根拠はありません。

おかきとおかきの衝突の結果について２種類の解釈を紹介しました。やはりメインは１＋１＝たくさんでしょう。

最近書いた記事：スター・ウォーズ/ スカイウォーカーの夜明けの神話解釈

四則演算

俯瞰

四則演算の計算方法を俯瞰してみましょう。

仮に全部解答がたくさんになるとします。それぞれのたくさんはなにが違うと言うのでしょう。

身体活動レベルの差

仮に同じおかきを潰して粉々にするとしても、小学生とスポーツ選手がやるのでは違った結果になります。

小学生低学年に砕かせても、そもそもうまく砕けなかったり、ひびが入るだけに終わったり、砕けても大きなかけらが残る形で砕くでしょう。

スポーツ選手に同じことをやらせるともちろんそうはなりません。特に力士とか、重量級の格闘家などがおかきを潰すとかなり細かく砕けるでしょう。念入りに潰してくださいと頼むと、細かくなりすぎてぱらぱらになると思います。

• 乳幼児や小学校低学年の子どもくらい力が弱い人
• 小学校中学年から中学生の子どもくらい力が弱い人
• 高校生以上の大人くらいには力が強い人
• スポーツ選手くらいには力が強い人

スポーツ選手が潰すとパラパラになることから、一番爆発力がある。よって乗算っぽい。

高校生以上の大人はパラパラにはならないが、普通に砕けそう。なので加算っぽい。

小学校中学年から中学生くらいの子どもは大人と比べて、砕けても大きな塊が残りそう。大人に劣るので減算っぽい。

乳幼児や小学校低学年の子どもは割れるか割れないかが問題です。よって除算っぽい。

おかきルールで二等辺三角形の面積を求めてみる

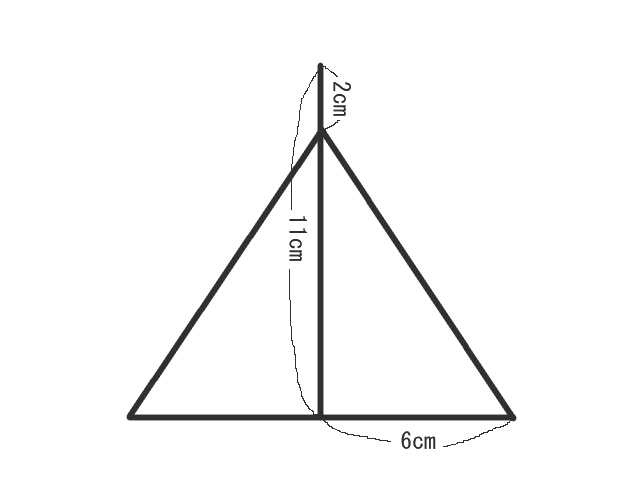
二等辺三角形の面積は底辺×高さ÷２です。上の図形から考えられる式とその解答は以下のようになります。

解答：（６×２）×（１１ー２）÷２＝１２×９÷２＝たくさん

最初の括弧の（６×２）ではスポーツ選手が６個と２個のおかきを潰して粉々にしたようです。さすがのスポーツ選手でも６個対２個だと、破片は残るかもしれません。潰すときの厳密なルールがはっきりしないので謎です。おかきのサイズがもっと小さいとかのルールがあれば現実に６対２も無理なくできるでしょう。でもそれだとおかき同士ではなく手のひらによって潰されそうです。現実感はないですが、おかき同士が接触しない限りは潰してはいけないルールにしておきましょう。この場合（６×２）の２個の方のおかきのうち２個が完全に潰れ、６個の方のおかきは２個が完全に潰れ、残る４個は潰れずに残ったと考えてみます。潰れた４個のおかきはパラパラになるくらいまで潰されました。

同時に小学校中学年から中学生くらいの子どもが１１個のおかきと２個のおかきを衝突させて、合計１３個のうち４個を潰し、潰されたおかきを破片がごろごろ残る状態にしました。

１１個と２個のような均衡のとれない個数の場合は割れずに残る確率が高いとか、手からこぼれ落ちる確率が高いなどの要因があるかもしれません。難しそうなので今回はややこしい要因を除外して考えます。

スポーツ選手によって４個がパラパラになった合計８個分のおかきと、小中学生が４個を潰して破片がごろごろ残る状態にした合計１３個のおかきを、スポーツ選手が叩いて潰すようです。この時ぱらぱらなおかきと、ごろごろになったおかきでは計算上何が違いそうでしょう。

• スポーツ選手が潰してぱらぱらになったおかきは相手側のおかきを潰す能力が５分の１になる。
• 大人が潰してぼちぼち砕けたおかきは相手側のおかきを潰す能力が５分の２になる
• 小中学生が潰して破片がごろごろ残るおかきは相手側のおかきを潰す能力が５分の３になる
• 幼児や低学年が潰して少し割れたおかきは相手側のおかきを潰す能力が５分の４になる

今適当に作った以上のルールが適用されるなら、４個のパラパラなおかきには０．８個のおかきを潰す能力があります。また、破片がごろごろになったおかきは２．２個のおかきを潰す能力があります。

合計８個でそのうち４個がパラパラなおかきは、相手方のおかきを潰す能力が合計４＋０．８＝４．８です。

合計１３個でそのうち４個がごろごろしているおかきは、相手方のおかきを潰す能力が合計９＋２．２＝１１．２です。

スポーツマンが潰した８×１３で合計２１個のおかきのうち４．２個だけが原形をとどめ、ほかの１６．８個はなにかしら砕けました。１６．８個のうちそれぞれどのような砕け方をしていそうでしょうか？

元々４個がパラパラに砕けていました。そこに新しくスポーツマンが４個の原形をとどめているおかきを９個のおかきに衝突させたので、新しく８個のおかきがぱらぱらになりました。最低１２個まではパラパラに砕けています。残った４．８個のうち４個は小中学生によって砕かれたごろごろしたおかきで、０．８個は４個分なパラパラおかきによって砕かれた分です。

０．８個のパラパラなおかきによって砕かれると、砕かれたおかきの『相手のおかきを砕く能力』はどうなるのでしょうか？　うーん、よく分かりません。仮に砕かれたおかきの『相手のおかきを砕く能力』は砕いた人の砕く能力に依存すると考えて、パラパラになることにしてみましょう。

２１個のおかきのうちわけ

• １２．８個がパラパラになっている
• ４個がゴロゴロしている
• ４．２個が原形をとどめている

計算に登場したすべてのおかきが減衰していかない様子がまるで、エントロピーってやつみたいです。食べれば減る。

最後の除算と解答

解答：（６×２）×（１１ー２）÷２＝１２×９÷２ ８×１３÷２＝２１÷２＝たくさん

２１÷２＝２３になります。エントロピー増大の法則（？）に慣れろと言うことみたいです。

２で除算なので２個のおかきと４．２個の原形をとどめているおかきのうちの２個を小さい子どもが衝突させて砕き、合計４個が小さく割れることになりました。

• １２．８個がパラパラになっている
• ４個が少し砕けている
• ４個がゴロゴロしている
• ２．２個が原形をとどめている

あれ？　二等辺三角形はどこへ行ったのですか？　それとも二等辺三角形の面積の１２．８個がパラパラになっているとでも言うのでしょうか？

誰にとって役に立つのか？

例えば警察にとっては窓ガラスや花瓶や食器等が割れている事件現場に遭遇したときに役立つでしょう。粉々になっている食器棚の食器が今回の計算と同じで１２．８個がパラパラになっており、４個が少し砕けており、４個がゴロゴロしており、２．２個が原形をとどめているとします。食器が１２．８個もパラパラになるまで粉砕されるとはずいぶん巨大な力によって砕かれたのでしょうか？　これはミステリーですね。

アスリートと小中学生がやってきて、食器棚の食器をそれぞれアスリート８枚、小中学生１３枚ずつ破壊し、その後アスリートは８枚の食器のうちの原形をとどめていた食器４（＋０．８）個と１３個の食器のうちの原形をとどめていた９（＋２．２）個との双方を叩き合わせ、その後乳幼児がやってきて食器棚に残っていた２枚の食器で２１個分の砕けている食器のうちの原形をとどめている４．２個を砕いたのかもしれません。

一体現実には何があったんでしょうか・・・。新しい推理小説が書けそうです。

スポーツ選手にとっても役に立つでしょうね。たぶん。

結局１＋１の正しい解答は？

１＋１はルールによって解答が変化するゲームの一種であると考えられます。

解答はルールの数だけあるのです。

以前何かのサイトでゲームの最小要素は以下の３つだと知りました。

• ルール
• 評価基準
• 結果

既存の数学は１＋１＝２を基本ルールとしている上位概念１＋１のローカルゲームの一種だと考えられます。ローカルゲームの１つだけを極めているようでは知的レベルに限界があるのです。

ゲームと言うことなので数学ではなく数楽にしたほうが、生徒も喜ぶでしょう。

最近書いた記事：がんばっていきまっしょい（映画）の神話解釈

小一の時点から教えるべき

今回の記事についてテレパシーは次のように述べています。

そういうことらしいので、教育委員会に知人がいましたらこの問題を教えてあげてください。小学一年生の時点から生徒には１＋１の解答が複数あることくらいは教えるべきでしょう。１＋１の解答が２だけであると信じさせる教育は非常に有害であり、このままでは知的レベルが低いと言う理由で人類は滅亡する可能性があります。

あ、それとミステリー小説の作家にも教えてあげてください。

※余談：テレパシーがどこかげっそりしているのは、毎日毎日悪魔たちが私とテレパシーとの間に味方同士で争い合わせるタイプの計略を仕掛け続けてきているためです。これだけ警戒しているのに、定期的に計略にかかるあたりかなり強力な悪魔が来ています。この１＋１についての情報はかなり人類に知られたくないようです。ぜひ拡散してください。私は本職の悪い軍師に計略をかけられると、簡単にかかるくらいには知的レベルが低いです。もう少し賢くならないとダメでしょう。

まとめ

おかきを砕くだけの話なのに、砕けたおかきの内訳が数式によって変わる。かなり奥が深そうな学問であることが分かりました。数式を数学者にしか分からない難しい数式にするとどうなるでしょうか。計算方法も今回適当に考えたものなので、本職の人たちが実際はどのような計算方法を考えるのかも気になるところです。

ちなみに今回の計算方法は囲碁の『絶対計算』なる計算方法を応用しました。気になる人は王銘エン九段の『ヨセ・絶対計算』を読んでください。

• おかきとおかきを衝突させると、粉々になってたくさんになるか、おかきとしての特性を失っておかきは消滅するか。
• 解釈によって１＋１＝たくさんや１＋１＝０などの式と解答になる
• 加算（足し算）は大人がおかきを叩き潰したような状態
• 減算（引き算）は小中学生、乗算（かけ算）はスポーツ選手、除算（割り算）は小さい子どもがおかきを叩き潰したような状態・・・かもしれない
• 少し複雑な数式を使うと、「たくさん」の内訳も複雑になる
• 何らかの職業の人にとっては役に立つので、小学校の時点から簡単なことは教えたい

最近書いた記事：四月物語（映画）の神話解釈